スペックの活用

このページに直接来られた方は，こちらからトップページが表示できます。

本書の最終章では，スペックの活用例を挙げています。具体的な設計課題を挙げて，各スペックを横断的に活用します。

オペアンプのスペック項目は，様々なアプリケーションに活用できます。この最終章では，オペアンプの基本回路である反転・非反転増幅器への活用例を主に示しています。ここで挙げる活用例は，それぞれのアプリケーションへの応用の参考になるでしょう。

最終章で挙げている設計課題とそのアウトラインを，以下に示します。

**① 直流出力電圧の計算**
下図の回路で，スペック項目の影響（入力オフセット電圧, オープンループ・ゲイン, CMRR, PSRR, 入力バイス電流, 入力オフセット電流）を含めた出力電圧を機械的に計算します。画像が表示されない場合は，こちらをクリック(.JPG)してください。図の回路で電源電圧を含めて任意に選ばれるとき、出力電圧の誤差要因には入力オフセット電圧だけでなく，いくつものスペック項目が絡みます。また両電源と単一電源とでは計算方法が異なりますから、両者について説明します。本書では，出力電圧の機械的な計算方法を示します。もちろん「計算結果と実測結果が，高精度に一致する」ことを示します。数値例は，こちらの第6, 7, 8章でご覧いただけます。

**② 抵抗負荷駆動で発生する直流誤差電圧の計算**
任意の抵抗値の負荷を接続したときの出力電圧の変化を計算します。「負荷起因での出力誤差電圧の計算」ともいえます。「低抵抗負荷」や「変動する負荷」で目立つ誤差要因です。画像が表示されない場合は，こちらをクリック(.JPG)してください。スペックの出力抵抗（オープン・ループ）から，クローズド・ループでの出力抵抗を計算して目的の出力電圧変化を計算します。しかし直流領域のオープン・ループ出力抵抗は，単純な理論展開に基づく計算には乗りません。本書では，広範囲に応用できる具体的な解決策を示します。もちろん「計算結果と，実測結果が一致する」ことを示します。

**③ 非反転増幅器の入力抵抗を含めた入力電圧の計算**
大きな入力抵抗が期待される非反転増幅器で，下図の信号源抵抗Rgが大きく非反転増幅器の入力抵抗が無視できない場合があります。そこで，「スペックの入力抵抗」から「非反転増幅器の入力抵抗」を算出し，Rgと非反転増幅器の入力抵抗による分圧を考慮した非反転入力端子の実質的な入力電圧を計算します。画像が表示されない場合は，こちらをクリック(.JPG)してください。スペック項目の入力抵抗から，非反転増幅器の入力抵抗を機械的に計算します。もちろん「計算結果が，実測結果と一致する」ことを示します。非反転増幅器の入力抵抗が分かれば，信号源抵抗との分圧として正確な非反転入力電圧が計算できます。この入力電圧を上記①に代入すれば，正確な出力電圧が計算できます。

**④ 直流シグナルゲインの計算**
反転・非反転増幅器の精密な直流シグナルゲイン（電圧増幅度）を，計算します。画像が表示されない場合は，こちらをクリック(.JPG)してください。入門書などでは「シグナルゲインは，非反転増幅器が1+R_f/R_Sで，反転増幅器は-R_f/R_S」と説明されますが，これは理想オペアンプが前提です。高精度増幅器やシグナルゲインの大きな反転・非反転増幅器では，現実のオペアンプが持つ誤差要因（スペック）が無視できなくなります。スペックを含めた精密な直流シグナルゲインを機械的に計算します。もちろん「計算結果が，実測結果と一致する」ことを示します。

**⑤ 直流出力電流変化に伴う出力電圧変化の計算**
出力電流変化に対する出力電圧変化を計算します。「ロード・レギュレーション」ともいい得ます。画像が表示されない場合は，こちらをクリック(.JPG)してください。これは，上記②の形を変えたものです。同様に，非直線性に配慮した計算方法で出力電圧変化を計算します。もちろん「計算結果が，実測結果と一致する」ことを示します。

**⑥ 直流特性の非直線性**
直流スペックが持つ，非直線性について解説しています。例えばオープンループ・ゲインやCMRRも，程度の差こそあれ非直線性を持ちます。これらが非直線性を持つことは，入力電圧や出力電圧などの動作条件によって誤差電圧が非直線的に変化することになります。またアプリケーションによっては，危険な非直線性も存在します。このような非直線性が持つ問題点を，横断的に解説しています。

**⑦ その他の直流誤差要因**
スペックには現れない誤差要因について説明しています。熱起電力や雑音や発振や漏れ電流など，オペアンプのスペックには現れませんが直流性能に影響を与える誤差要因があります。これら誤差要因と，その対策を解説しています。

⑧ 交流シグナルゲインと位相差の計算

反転・非反転増幅器の交流シグナルゲイン（電圧増幅度）や入出力間の位相差を，任意の周波数で計算します。交流においても，表計算ソフトや電卓などを用いて機械的に計算できます。

計算式には，オペアンプの周波数特性を組み込んでいます。ですから，オペアンプの誤差要因を含めた正確な計算ができます。帰還回路は下図のとおりで，静電容量を0[F]で計算すれば，抵抗器のみの帰還回路としても計算できます。

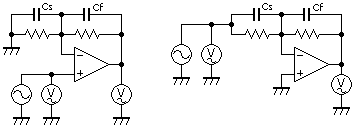
画像が表示されない場合は，こちらをクリック(.JPG)してください。

計算結果と実測結果の一例を示します。上図の回路で，帰還コンデンサ（Cf）を0[μF]と0.1[μF]の二通りで10[kHz]において実験しました。なお，Cs=0[μF]で，直流シグナルゲインは反転増幅器が-1[V/V], 非反転増幅器が+2[V/V]です。

シグナルゲイン（|a_CL|）と位相（θ）の計算結果は，次表の通りです。

Cf	0[μF]		0.1[μF]
\|a_CL\| or θ	\|a_CL\|[V/V]	θ[deg]	\|a_CL\|[V/V]	θ[deg]
反転増幅器	-0.999	-0.35	-0.846	-32.5
非反転増幅器	+1.99	-0.35	+1.77	-15.1

反転増幅器の実測結果は，次の通りです。

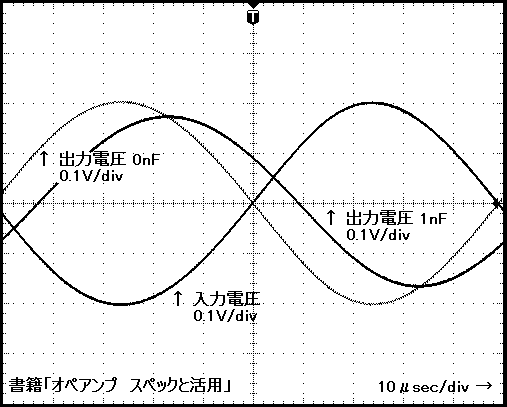
画像が表示されない場合は，こちらをクリック(.JPG)してください。

非反転増幅器の実測結果は，次の通りです。

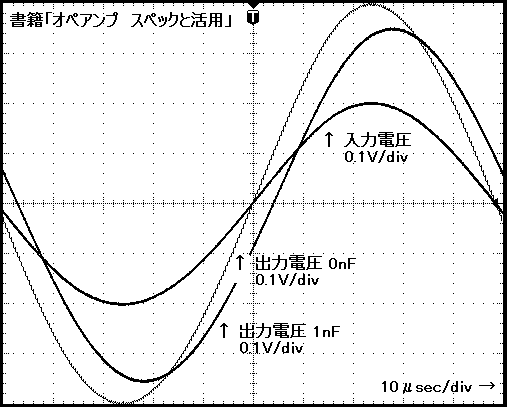画像が表示されない場合は，こちらをクリック(.JPG)してください。

実測結果と計算結果は，一致しています。

上記の例は，信号周波数が10[kHz]です。更に周波数が高くなると，オペアンプ単体の位相回転が大きくなり，単純な理論展開では計算に乗らなくなります。新たに管理すべきパラメーターが発生しますが，高域における計算方法も示しています。上記と同じオペアンプを，ユニティーゲイン・アンプとして1[MHz]で検証した例（下図）を次に挙げます。

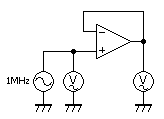
画像が表示されない場合は，こちらをクリック(.JPG)してください。

シグナルゲイン（|a_CL|）と位相（θ）の計算結果は，次表の通りです。

\|a_CL\|[V/V]	θ[deg]
1.05	-24.2

この計算結果は，|a_CL|が+1[V/V]よりも大きくなっており，ピーキング特性をうかがわせます。
実測結果は，次の通りです。

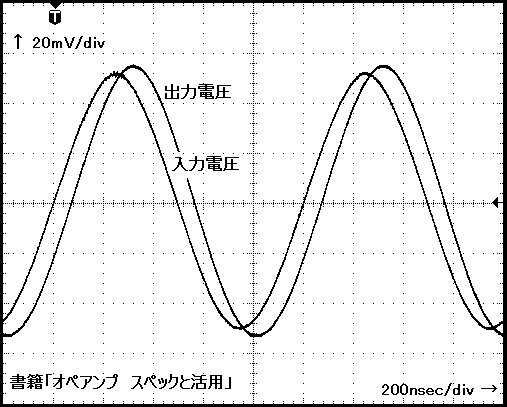
画像が表示されない場合は，こちらをクリック(.JPG)してください。

実測結果と計算結果は，一致しています。

**⑨ インピーダンス負荷駆動で発生する振幅誤差と位相誤差の計算**
任意の抵抗値および静電容量の負荷を接続したときの交流出力電圧振幅と位相の変化を機械的に計算します。「負荷起因の誤差計算」ともいえます。"低インピーダンス負荷"や"変動する負荷"で目立つ誤差要因です。画像が表示されない場合は，こちらをクリック(.JPG)してください。スペックの出力抵抗（オープン・ループ）からクローズド・ループ出力インピーダンスを計算し，目的の出力電圧変化を計算します。

⑩ 交流出力電流に伴うリプル電圧の計算

オペアンプ出力に交流電流が流れ込むときに，出力端子に現れるリプル電圧の大きさと位相を機械的に計算します。

画像が表示されない場合は，こちらをクリック(.JPG)してください。

これは，上記⑨の形を変えたものです。スペックの出力抵抗からクローズド・ループ出力インピーダンスを計算し，そこへ交流電流を通じたときに発生する電圧を計算します。計算結果は，電圧振幅と交流電流を0°とする位相として表します。
例えば，下のオシロスコープの画像は実測結果ですが，この計算結果は次表のとおりでした。

Cf	0[nF]	1[nF]
V_RIPPLE	272[mV_PEAK]	209[mV_PEAK]
Phase	+72.6°	+47.0°

リプル電圧の実測結果

画像が表示されない場合は，こちらをクリック(.JPG)してください。

検証結果には歪みを伴っていますが，概ね実測結果と計算結果は一致しています。歪みの発生メカニズムは，本書の中で解説しています。

**⑪ 静電容量負荷における計算**
「静電容量負荷による発振までの余裕」を計算で評価します。任意の静電容量負荷と帰還回路における余裕を，ループゲインと位相の両面からの計算で見積もります。しかし静電容量負荷による発振には，単純な位相回転によらない発振モードがいくつかあります。こうした発振は計算に乗らないので，応用にあたっては注意が必要です。本書では，このような事例を5例挙げて，そのメカニズムを解説しています。

**⑫ 方形波応答の計算**
反転・非反転増幅器を用いた方形波の応答特性では，単にスルーレートにとどまらない興味深い関係式を得ることができました。計算結果と実測結果が一致することを示します。

**⑬ ヒステリシス特性の計算**
反転・非反転増幅器で入出力電圧の動特性を精密に追うと，ヒステリシス特性を持つように見えます。理論的に解析した計算式によってヒステリシスの大きさを求め，実測結果と一致することを示します。

⑭ 増幅器出力の雑音の実効値

反転・非反転増幅器で，その出力に現れる白色雑音電圧の実効値をオペアンプの等価入力雑音電圧などから機械的に計算します。

画像が表示されない場合は，こちらをクリック(.JPG)してください。

上図において帰還コンデンサCfの有無による出力雑音の違いを等価入力雑音電圧と周辺回路の部品定数に基づいて計算し，実測を行いました。結果は，次表のとおりです。

Cf	0[nF]	1[nF]
計算結果	157[μVrms]	36.6[μVrms]
実測結果	155[μVrms]	34.5[μVrms]

これら数値は，多くのアプリケーション設計で実用的な精度に収まっていると思います。

**⑮ 抵抗器∥コンデンサ回路が発生する熱雑音の計算**
抵抗器に並列コンデンサを取り付けた回路で，任意の周波数帯域幅における雑音電圧の実効値などを計算します。画像が表示されない場合は，こちらをクリック(.JPG)してください。オペアンプの周辺回路や信号源が発生する熱雑音の計算に用います。

**⑯ 帰還回路の並列コンデンサCfの計算**
反転・非反転増幅器の雑音低減方法の一つが，下図の並列コンデンサCfの利用です。画像が表示されない場合は，こちらをクリック(.JPG)してください。しかし，このCfは信号振幅にも影響を与えます。そこで，信号周波数と信号の振幅誤差を定めて，Cfの逆算方法を示します。

**⑰ 任意のしきい値を超える雑音の発生確率**
任意の振幅を超える白色雑音の発生確率を，機械的に計算します。画像が表示されない場合は，こちらをクリック(.JPG)してください。例えば，上図は34.5[μVrms]の白色雑音電圧ですが，この雑音電圧が100[μV]を超える"発生確率"として求めます（±3[div]を超える振幅が占める時間割合）。この例では，計算結果が0.38[%]であり，実測結果は0.44[%]でした。「100秒間のうち，0.4秒程度は100[μV]を超える」といえます。計算結果は，実用的な精度に収まっていると思います。

**⑱ 半導体を通じる電流に伴う雑音**
入力バイアス電流のように，半導体を通じる電流起因で発生する雑音電流の実効値を計算します。これはショット雑音のそれです。本書では，ショット雑音の計算結果と実際とがよく符合することを実測を通して示します。

**⑲ 等価雑音帯域幅の計算**
雑音測定で不可欠な等価雑音帯域幅の計算方法を示します。等価雑音帯域幅とは，下図のようにスカート特性を持つフィルターに白色雑音を入力して，その出力に現れる雑音と同じ大きさの雑音が得られる矩形状のフィルターの（仮想の）帯域幅のことです。下図の場合，その等価雑音帯域幅は110[Hz]です。画像が表示されない場合は，こちらをクリック(.JPG)してください。等価雑音帯域幅は，積分計算を伴います。一次CRフィルター程度であれば，積分計算もできます。しかしフィルターの次数が高くなると，高次有理関数の積分となり，その計算は容易ではありません。そこで実用的な方法を紹介しています。また，アクティブ・フィルターの伝達関数を求め，その等価雑音帯域幅を計算します。伝達関数からは，アクティブ・フィルターの振幅特性[V/V]や位相特性[°]も計算できます。また，そのままでは精密な特性の把握が難しいLPF特性の精密測定方法も紹介しています。等価雑音帯域幅を使わない場合も，アクティブ・フィルターの設計にも役立てることができます。